Big O notation or Big Oh notation, and also Landau notation or asymptotic notation, is a mathematical notation used to describe the asymptotic behavior of functions. Its purpose is to characterize a function's behavior for very large (or very small) inputs in a simple but rigorous way that enables comparison to other functions. More precisely, the symbol O is used to describe an asymptotic upper bound for the magnitude of a function in terms of another, usually simpler, function. There are also other symbols o, Ω, ω, and Θ for various other upper, lower, and tight bounds. It has two main areas of application: in mathematics, it is usually used to characterize the residual term of a truncated infinite series, especially an asymptotic series, and in computer science, it is useful in the analysis of the complexity of algorithms.
Informally, the O notation is commonly employed to describe an asymptotic tight bound, but tight bounds are more formally and precisely denoted by the Θ (capital theta) symbol as described below.
It was first introduced by German number theorist Paul Bachmann in 1894, in the second volume of his book Analytische Zahlentheorie ("analytic number theory"), the first volume of which (not yet containing big O notation) came out in 1892. The notation was popularized in the work of another German number theorist Edmund Landau, hence it is sometimes called a Landau symbol. The big-O, standing for "order of", was originally a capital omicron; today the identical-looking Latin capital letter O is also used, but never the digit zero.
Uses
There are two formally close, but noticeably different usages of this notation: infinite asymptotics and infinitesimal asymptotics. This distinction is only in application and not in principle, however—the formal definition for the "big O" is the same for both cases, only with different limits for the function argument.
Infinite asymptotics
Big O notation is useful when analyzing algorithms for efficiency. For example, the time (or the number of steps) it takes to complete a problem of size n might be found to be T(n) = 4n² - 2n + 2.
As n grows large, the n² term will come to dominate, so that all other terms can be neglected—for instance when n = 500, the term 4n² is 1000 times as large as the 2n term, and so ignoring the latter would have negligible effect on the expression's value for most purposes.
Further, the coefficients become irrelevant as well if we compare to any other order of expression, such as an expression containing a term n³ or 2n. Even if T(n) = 1,000,000n², if U(n) = n³, the latter will always exceed the former once n grows larger than 1,000,000 (T(1,000,000) = 1,000,000³ = U(1,000,000)).
So the big O notation captures what remains: we write

(pronounced "big O of n squared") and say that the algorithm has order of n² time complexity.
Infinitesimal asymptotics
Big O can also be used to describe the error term in an approximation to a mathematical function. For example,

expresses the fact that the error, the difference  , is smaller in absolute value than some constant times |x|3 when x is close enough to 0.
, is smaller in absolute value than some constant times |x|3 when x is close enough to 0.
Formal definition
Suppose f(x) and g(x) are two functions defined on some subset of the real numbers. We say

if and only if

The notation can also be used to describe the behavior of f near some real number a: we say

if and only if

If g(x) is non-zero for values of x sufficiently close to a, both of these definitions can be unified using the limit superior:

if and only if


Theory of O-Notation: f is in the order of g (f(x) = O(g(x))) if and only if there exists a positive real number M and a real number x0 such that for all X,
|f(x)| <= M . |g(x)|, wherever x > x0
In mathematics, both asymptotic behaviours near ∞ and near a are considered. In computational complexity theory, only asymptotics near ∞ are used; furthermore, only positive functions are considered, so the absolute value bars may be left out.
Example
Take the polynomials:


We say f(x) has order O(g(x)) or O(x4). From the definition of order, |f(x)| ≤ C |g(x)| for all x>1, where C is a constant.
Proof:
 where x > 1
where x > 1
 because x3 < x4, and so on.
because x3 < x4, and so on.

 where C = 13 in this example
where C = 13 in this example
Matters of notation
The statement "f(x) is O(g(x))" as defined above is usually written as f(x) = O(g(x)). This is a slight abuse of notation; equality of two functions is not asserted. The property of being O(g(x)) is not symmetric:
 .
.
For this reason, some authors prefer set notation and write 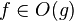 , thinking of O(g) as the set of all functions dominated by g.
, thinking of O(g) as the set of all functions dominated by g.
In more complex usage, O( ) can appear in different places in an equation, even several times on each side. For example, the following are true for 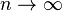
- (n + 1)2 = n2 + O(n)

- nO(1) = O(en)
The meaning of such statements is as follows: for any functions which satisfy each O( ) on the left side, there are some functions satisfying each O( ) on the right side, such that substituting all these functions into the equation makes the two sides equal. For example, the third equation above means: "For any function f(n)=O(1), there is some function g(n)=O(en) such that nf(n)=g(n)." In terms of the "set notation" above, the meaning is that the class of functions represented by the left side is a subset of the class of functions represented by the right side.
Common orders of functions
Here is a list of classes of functions that are commonly encountered when analyzing algorithms. All of these are as n increases to infinity. The slower-growing functions are listed first. c is an arbitrary constant.
Not as common, but even larger growth is possible, such as the single-valued version of the Ackermann function, A(n,n). Conversely, extremely slowly-growing functions such as the inverse of this function, often denoted α(n), are possible. Although unbounded, these functions are often regarded as being constant factors for all practical purposes


















 paros_3.2.9_win.exe
paros_3.2.9_win.exe paros_user_guide.pdf
paros_user_guide.pdf

 , is smaller in
, is smaller in 







 where x > 1
where x > 1
 because x3 < x4, and so on.
because x3 < x4, and so on.

 where C = 13 in this example
where C = 13 in this example  .
. 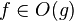 , thinking of
, thinking of